在js中只有number类型,没有进行整数和浮点数的区分
而在js的内部,number是采用 IEEEF 754 规范 中的64位双精度浮点数进行编码的,所以 1 === 1.0 是为true的, 也就是说 js 语言底层根本没有整数, 所有数字都是64位双精度浮点数. (容易造成混淆的是位运算只有整数才能完成,此时js会自动把64位双精度浮点数,转换为32位整数)
IEEE 754
IEEE 二进制浮点数算术标准 是20世纪80年来以来最广泛使用的浮点数运算标准,为许多 CPU 与 浮点运算器所采用,这个标准定义了 浮点数的格式(包括负零 -0)、反常值、一些特殊值(无穷、非数值),以及这些值的浮点运算符.
IEEE 754 规定了四种表示浮点数值的方式: 单精度(32位)、双精度(64位)、延伸精度(43位以上,很少使用)与延伸双精度(79位以上,通常以80位实现)
浮点数剖析
value = sign * exponent * fraction
也就是浮点数的实际值 等于 符号位(sign) 乘以 指数偏移量 乘以 分数值
这里解释一下:
我们都知道科学计数法, 即把一个数比如: 123465.555 可以写作 1.2346555*105,类比十进制的写法,比如 16.25(十进制) => 10000.01 可以写作 1.000001 * 24,那么他的分数值即为 000001(整数位省略,下文会讲到), 指数为 4(这里不是指数偏移量)
整体呈现
二进制浮点数是以 有符号数值表示法(0 表示一个正数 1表示一个负数) 的储存格式,即最高位被指定为符号位(sign bit),"指数部分" 即次高位 有效的 e 个比特 存储指数,最后剩下的 f 个低有效的比特,存储"有效数"的小数部分(即上边科学计数法表示的分数值,在非规约形式下整数默认为0,其他情况下默认为1)

指数偏移值
指数偏移值,即浮点数表示法中指数域的编码值,等于指数的实际值 加上某个固定值 IEEE 754标准规定该值固定为 2e-1 -1,其中e为存储指数的比特长度
以单精度浮点数为例,它的指数域为 8 个比特,那么它的固定偏移值为 28-1 - 1 = 128 - 1 = 127, 此为"有号数的表示方式", 单精度浮点数的指数部分实际取值是从 -126到127(-127 和 128 被用作特殊值处理, 见下方 非规约形式的浮点数 和特殊值),比如指数的实际值为 17 在单精度浮点数中指数的编码值为144 即 144 = 17 + 127.
采用指数的实际值加上固定偏移值的办法表示浮点数的指数,好处是可以用长度为 e 个比特的无符号整数 来表示所有指数的取值,这使得两个浮点数的指数大小比较更为容易,这里移码表示的指数部分 也称作阶码
规约形式的浮点数
如果浮点数中的指数部分的编码值在 0 < exponent < 2****e **-2 之间, 且在科学表示法的表示形式下,分数(fraction)部分最高有效位(即整数字)为1,**那么这个浮点数被称为 规约形式的浮点数,
由于这种表示下的尾数有一位隐含的二进制有效数字,为了与二进制科学计数法的尾数相区别,IEEE 754称之为有效数.(这里解释一下,上文已经说到 fraction 域 存储的为 "有效数"的小数部分,即整数部分 0非规约情况下 或 1其它情况下 是省略的 所以说有一位隐含的二进制有效数字 )
举例来说 单精度(32-bit)的规约形式浮点数 在指数偏移值的值域大小为 00000001 - 11111110,在分数部分则是 0000....000 - 1111....1111(23比特)
非规约形式的浮点数
如果浮点数的**指数部分的编码为0,分数部分非0,**那么这个浮点数被称作非规约浮点数,一般是某个数字相当接近零时,才会使用非公约形式来表示,IEEE 754 规定表示: 非规约形式的浮点数的指数偏移值比规约形式的浮点数的指数偏移值小1,
例如: 最小规约形式的单精度浮点数的指数域编码值为 1, 指数的实际值为 -126,而非规约的单精度浮点数的指数域编码值为 0,对应的指数的实际值也是 -126 而不是 -127.
实际上非规约形式的浮点数仍然是有效可以使用的,只是它们的绝对值已经小于所有的规约浮点数,即所有的非规约浮点数比规约浮点数更接近 0,规约浮点数的尾数大于1,且小于2,而规约浮点数的尾数小于 1 且大于0.
特殊值
1. 如果指数是 0 且 尾数的小数部分是0,那么这个数为 ±0(正负与符号位有关)
2. 如果指数 = 2e - 1,并且尾数的小数部分是0 这个数为 ±∞ (正负与符号位有关)
3. 如果指数 = 2e -1,并且尾数的小数部分非 0, 这个数表示为非数(NaN)
64位双精度
双精度二进制小数,使用64个比特储存

S 为符号位,Exp 为指数字,Fraction 为有效数字,指数部分即使用所谓的偏正值表示,偏正值为实际指数的大小与一个固定的值(64位的情况是1023)的和,
采用这种方式表示的目的是为了简化比较,因为指数的值也可能为负数也可能为正数,如果采用补码的方式表示的话,全体符号位S和Exp自身的符号位将导致不能简单的比较大小,正因为如此,指数部分通常采用一个无符号的整数值储存,双精度的指数部分是 -1022 至 +1023 加上1023,指数值得大小从1 至 2046( 0 2进制位全为0 和2047 2进制全为1 是特殊值),浮点小数计算时,指数值减去偏正值将是实际的指数大小.
浮点数的比较
浮点数基本上可以按照符号位、指数域、尾数域的顺序做字典比较,显然,所有正数大于负数,正负号相同时,指数的二进制表示法更大的其浮点数的值更大
浮点数的舍入
比如64位双精度浮点数 的尾数为52位, 32位单精度浮点数的 尾数位为23位,浮点数格式的表示的精度是有限的,当转换为浮点数格式时,多余的比特必须丢弃,IEEE 754标准给出了 四种 不同的舍入作业方法:
1. 舍入到最近(默认):舍入到最近,在一样接近的情况下偶数优先: 会将结果舍入为最接近且可表示的值,但是当两个数一样的时候,则取其中的偶数(二进制中以0结结尾),也叫做向偶数舍入
2. 朝 正∞ 方向舍入:将结果向正无穷方向舍入,也叫做向上舍入
3. 朝 负∞ 方向舍入:将结果向负无穷方向舍入,也叫做向下舍入
4. 朝 0 方向舍入:将结果向0舍入,也叫做向0舍入
下边是四种舍入方式的应用举例:
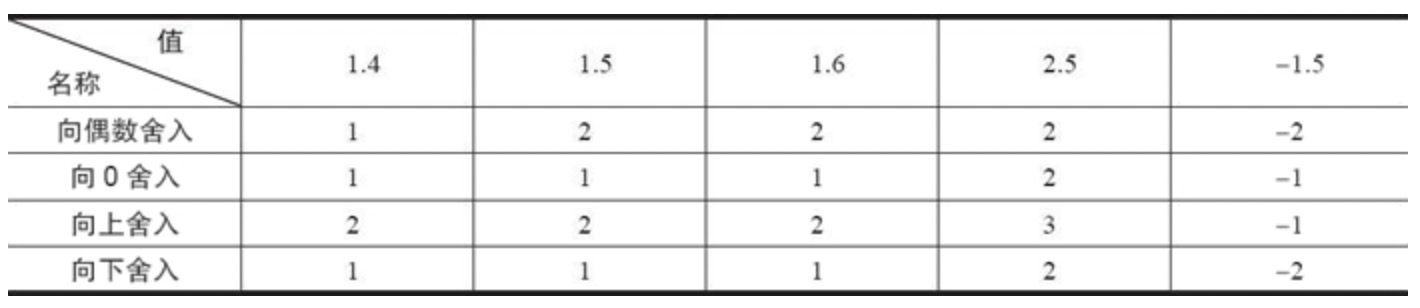
这里解释一下舍入到最近:
也许看了上边的内容你会问:为什么采用向偶舍入,而不是直接采用我们已经习惯的"四舍五入"呢?
其原因可以这样理解,在进行舍入的时候,最后一位数字从 1 到 9,舍去的有1、2、3、4,它正好可以和进位的9、8、7、6相对应,而5却被单独留下来进行进位了,如果采用四舍五入每次将5进位的话,在进行大量数据统计的时候,就会积累比较大的偏差,而采用向偶数舍入的策略时,在绝大多数情况下,5舍去还是进位的概率是差不多的,进行大量数据计算是产生的偏差相应较小
在十进制的情况下:
例如
1.234999 舍入为 1.23,
1.2350001 舍入为 1.24
对于 1.23499,1.23和1.24 相比,1.23距离原数 1.234999 最近
对于 1.2350001,1.23和1.24相比,1.24距离原数 1.2350001 最近
1.2350000 舍入为 1.24
这里对于原数1.235000, 1.23和.124距离原数相等,但是 4 为偶数所以 舍入为 1.24
在二进制的情况下:
例如
1.001 011 舍入为 1.001
|1.001 - 1.001 011| = 0.000 011
|1.010 - 1.001 011| = 0.000 100
明显可以看到前边的值更接近原始值,因此舍入后的结果为 1.001
1.001 101 舍入为 1.010
|1.010 - 1.001 101| = 0.000 010
|1.001 - 1.001 101| = 0.000 101
明显可以看到前边的值更接近原始值,因此舍入后的结果为 1.010
由此我们可以总结出两条规律:
当有效位的后一位是 0 时,此时即将被舍去的值小于一半,那么应该向下舍入,
当有效位的后一位是 1 时,而且后面的数位不全为 0 时, 此时将被舍去的值大于一半,那么应该向上舍入
看完这两种情况,我们再来看特殊的情况,有效位后一位是 1,后边位数全部是 0 ,此时即将被舍去的值刚好是一半,此时我们需要选择向偶数舍入,即将数值向下或向上舍入,使得结果的最低有效位是偶数,在二进制的情况下就是为0,这样50%的概率它是向上舍入,50%的概率它是向下舍入,
1.001 100 舍入为 1.010
此时舍去100 之后进位的 1.010 和 1.001 距离1.001 100 是相等的,根据偶数舍入原则,取1.010
从这个例子我们可以看出:如果即将被舍去的值刚好为一半,此时,如果最低有效位为奇数,则向上舍入,如果为偶数,则向下舍入,从而实现使最低有效位始终为偶数
0.1+0.2
0.1+0.2=0.30000000000000004一直是一个经典的问题,甚至有个网站专门收录了各个语言0.1+0.2的计算结果 https://0.30000000000000004.com/
这里我们结合上述的IEEE 754标准手动计算一下
首先将0.1、0.2 转换为二进制,十进制小数转换二进制使用"乘2取整,顺序排列法"
0.1转换为二进制计算如下:
0.1 * 2 = 0.2 整数部分为 0
0.2 * 2 = 0.4 整数部分为 0
0.4 * 2 = 0.8 整数部分为 0
0.8 * 2 = 1.6 整数部分为 1
0.6 * 2 = 1.2 整数部分为 1
0.2 * 2 = 0.4 整数部分为 0
0.4 * 2 = 0.8 整数部分为 0
0.8 * 2 = 1.6 整数部分为 1
0.6 * 2 = 1.2 整数部分为 1
0.2 * 2 = 0.4 整数部分为 0
0.4 * 2 = 0.8 整数部分为 0
0.8 * 2 = 1.6 整数部分为 1
0.6 * 2 = 1.2 整数部分为 1
....
可得出 十进制的 0.1 转换为 二进制之后为 0.0 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 ... 0011的循环
既然为无限循环小数,那么在转换为浮点数进行存储的时候必然要发生舍入,
1. 我们把这个无限循环小数转换为科学计数法为 1.1 0011 0011 0011 0011 0011... * 2-4
2. 尾数部分储存的为分数(非规约整数默认为0,其他情况一律为1),那么分数部分储存的为 1 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011...
3. 尾数部分为52比特,则在舍入第53位即 001 ---- 1 此时按照有效位后一位为 1 时,且后边的数位不完全为0,向上舍入原则,
得出 最终舍入之后的二进制 0.1 为 0.0 001 1 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 010
0.2 同理得出为 0. 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 010
那么 二进制的 0.1 + 0.2 为
0.00011001100110011001100110011001100110011001100110011010
+ 0.00110011001100110011001100110011001100110011001100110100
注意:这里0.2的二进制是比0.1的二进制少一位的 所以需要补上一个0
得出结果为 0.01001100110011001100110011001100110011001100110011001110
转换为十进制为 0.30000000000000004
所以 0.1 + 0.2 的问题根本为 0.1 和0.2的二进制为无限循环小数,而js中储存数据采用的是64位双精度的浮点数,发生了舍入,所以导致了 0.30000000000000004 的结果
安全整数和数值范围
安全整数
根据 IEEE 754 标准 我们不难得出 超出尾数范围的数就会发生舍入,从而导致精度问题,所以在js中 安全数值的范围为 -253 至 253 之间 不含两个端点
1 Math.pow(2,53).toString(2) // "100000000000000000000000000000000000000000000000000000" 2 3 Math.pow(2,53).toString(2).length // "54" 4 5 (Math.pow(2,53)-1).toString(2) // "11111111111111111111111111111111111111111111111111111" 6 7 (Math.pow(2,53)-1).toString(2).length // 53 8
为什么是 53 呢,因为转换之后整数位是省略的 所以正好为 52位
验证安全整数的代码如下
1 Math.pow(2, 53) // 9007199254740992 2 3 9007199254740992 // 9007199254740992 4 9007199254740993 // 9007199254740992 5 6 Math.pow(2, 53) === Math.pow(2, 53) + 1 7 // true 8 9 Math.pow(2,53)-1 10 // 9007199254740991 11 12 Math.pow(2,53)-2 13 9007199254740990 14
数值范围
尾数部分控制精度,指数部分+尾数部分控制范围
最大值:64位双精度浮点数的指数域为11位,那么指数位的最大值为 211 - 1 = 2047 又因为指数域为无符号表示法,加上了固定数 1023, 所以指数部分最大值为 2047 - 1023 = 1024
即如果一个数大于等于 2 的1024次方就会发生正向溢出(也就是上述的特殊值)
测试代码如下
1 Math.pow(2,1024) // Infinity 2 3 Math.pow(2,1023) // 8.98846567431158e+307 4
这里可能有些疑问,为什么要这样去验证
这里解释一下,指数部分最大值为 1024 即 科学计数法时,小数点偏移的位置,即 x.xxx * 21024,
可以看这个例子
1 Math.pow(2,1023).toString(2) // 1000000000..... 2 Math.pow(2,1023).toString(2).length // 1024 3
2的 1023次方转换为 二进制的长度为 1024,那么此时转换为科学计数法为 1 * 21023
最小值得话就很简单,如果一个数小于等于2的-1075次方(指数部分最小值-1023,再加上小数部分的52位),那么就会发生负向溢出(这里有些理解错误,可以叫做接近0的最小值) js无法表示 这时会直接返回0(注意这里不是负无穷,表示的最小接近0的数 即 指数部分负向拉满,小数部分为0000000.....1)
1 Math.pow(2, -1075) // 0 2
所以js能够表示的数值范围为 21024到2-1075 不包含两个端点
参考链接:
https://zh.wikipedia.org/wiki/IEEE_754#%E6%B5%AE%E9%BB%9E%E6%95%B8%E5%89%96%E6%9E%90
https://javascript.ruanyifeng.com/grammar/number.html#toc1
https://my.oschina.net/u/4081479/blog/4670415
https://cloud.tencent.com/developer/article/1399432
https://fengmumu1.github.io/2018/06/30/js-number/
http://liguixing.com/archives/1284
https://juejin.cn/post/6844903620140335112